AS - example 4 - noise of current converter
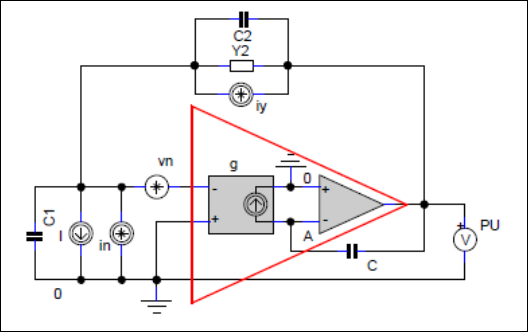
Figure 1: C:\jobs\Maxima\AS\ex\_img\ex4.png

Figure above (embedded only in *.wxmx file) shows a linear model of a current converter.
Transfer functions are processed below to calculate output noise.
| (%i94) |
/* working directory must be explicitly defined HERE ! */ kill(all) $ file_search_maxima : append(["c:/jobs/Maxima/AS/ex/libs/###.{mac,mc}"],file_search_maxima ) $ load("_myUnits") $ load("_myFunctions") $ /* suppress ratsimp warnings */ ratprint: false $ algebraic:true $ keepfloat:true $ fpprintprec: 4 $ /* GNU plot (default) or wxplot for 0 */ GNUPLOTFLAG: 0 $ wxplot_size:[800,400] $ /* Debug level 0 - none 3 - all */ DBG: 0 $ /* By default, all symbols, are considered to represent real numbers */ declare(s, complex) $ |

| (%i12) |
/* AS */ /* U=Kn*vn+M*I+Mn*in+My*iy */ Da: (s^(2)*(C1*C+C2*C)+s*(C*Y2+C2*g)+Y2*g) $ DbKn: (g)*(s*(C1+C2)+Y2) $ Kn:DbKn/Da $ DbM: (g)*(1) $ M:DbM/Da $ DbMn: (g)*(1) $ Mn:DbMn/Da $ DbMy: (g)*(1) $ My:DbMy/Da $ /* ------ */ Kn(s):=ratsimp(Kn) $ M(s):=ratsimp(M) $ Mn(s):=ratsimp(Mn) $ My(s):=ratsimp(My) $ /* circuit parameters */ R2: 100*kOhm $ Y2: 1/R2 $ C1: 5.8*pF $ C2: 0.76*pF $ /* OP-AMP */ ft: 16*MHz $ C: 3*pF $ GBW: 2*(%pi)*ft $ /* GBW = g/C */ g:GBW*C $ /* OP-AMP noise */ e_n: 16*nV $ F_ce: 1000*Hz $ i_n: 0.001 * pA $ F_ci: 1000*Hz $ /* noise bandwidth - limits for integration of noise density functions */ f_n1: 1 $ f_n2: 100*ft $ /* reference voltage noise density is a R noise */ e_R: sqrt(4*kT*R2) $ |
| (%i40) |
/* OP-AMP VOLTAGE NOISE CONTRIBUTION */ Se(f) := e_n^2*(1+F_ce/f) $ define(K_n(s),float(ratsimp(ev(Kn(s),[C=float(C), g=float(g), Y2=float(Y2), C2=float(C2), C1=float(C1)])))) $ DBG_2("Kn(s) = ",Kn(s)) $ DBG_2("K_n(s) = ",K_n(s)) $ gainK_n(f) := cabs(K_n(%i*2*%pi*f)) $ define(GK_n(f), float(ratsimp(gainK_n(f)))) $ DBE_2("GK_n(f) = ", GK_n(f)) $ define(S_e(f),float(ratsimp(ev(Se(f),[e_n=float(e_n),F_ce=float(F_ce)])))) $ DBG_2("S_e(f) = ", S_e(f)) $ Soe(f) := S_e(f) * (GK_n(f))^2 $ define(S_oe(f),float(ratsimp(Soe(f)))) $ DBG_2("S_oe(f) = ", S_oe(f)) $ /* OP-AMP CURRENT and Y CURRENT NOISE NOISE CONTRIBUTION */ Si(f) := i_n^2*(1+F_ci/f) $ Sy(f) := 4*kT*Y2 $ define(M_n(s),float(ratsimp(ev(Mn(s),[C=float(C), g=float(g), Y=float(Y), Y2=float(Y2), C2=float(C2), C1=float(C1)])))) $ DBG_2("M_n(s) = ",M_n(s)) $ gainM_n(f) := cabs(M_n(%i*2*%pi*f)) $ define(GM_n(f), float(ratsimp(gainM_n(f)))) $ DBG_2("GM_n(f) = ", GM_n(f)) $ define(S_i(f),float(ratsimp(ev(Si(f),[i_n=float(i_n),F_ci=float(F_ci)])))) $ define(S_y(f),float(ratsimp(ev(Sy(f),[kT=float(kT),Y2=float(Y2)])))) $ DBG_2("S_i(f) = ", S_i(f)) $ DBG_2("S_y(f) = ", S_y(f)) $ Soi(f) := S_i(f) * (GM_n(f))^2 $ define(S_oi(f),float(ratsimp(Soi(f)))) $ DBG_2("S_oi(f) = ", S_oi(f)) $ Soy(f) := S_y(f) * (GM_n(f))^2 $ define(S_oy(f),float(ratsimp(Soy(f)))) $ DBG_2("S_oy(f) = ", S_oy(f)) $ |
| (%i69) |
/* power noise density integration */ key:1 $ intE:quad_qag(S_oe(f),f,f_n1,f_n2,key) $ ve_uV:float(sqrt(ev(intE[1]))/uV) $ intI1:quad_qag(S_oi(f),f,f_n1,f_n2,key) $ vi_uV:float(sqrt(ev(intI1[1]))/uV) $ intY1:quad_qag(S_oy(f),f,f_n1,f_n2,key) $ vy_uV:float(sqrt(ev(intY1[1]))/uV) $ /* total voltage noise i_n f_n2-f_n1 bandwidth */ vo_uV:float(sqrt(vy_uV^2 + vi_uV^2 + ve_uV^2)) $ |
| (%i77) |
print("R2 = ", R2/kOhm, "[kOhm]") $ print("C1 = ", C1/pF, "[pF]") $ print("C2 = ", C2/pF, "[pF]") $ print("ft = ", ft/MHz, "[MHz]") $ print("C = ", C/pF, "[pF]") $ print("g = ", float(g/mS), "[mS]") $ print("e_n = ", e_n/nV, "[nV/sqrt(Hz)]") $ print("F_ce = ", F_ce, "[Hz]") $ print("i_n = ", i_n/pA, "[pA/sqrt(Hz)]") $ print("F_ci = ", F_ci, "[Hz]") $ |
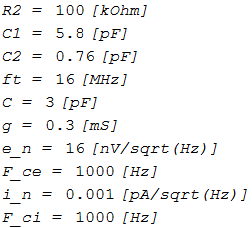
| (%i87) |
print("vo = sqrt(ve^2+vi^2+vy^2) = ", vo_uV, "[uV]") $ print("vE = ", ve_uV, "[uV]") $ print("vI = ", vi_uV, "[uV]") $ print("vY = ", vy_uV, "[uV]") $ |
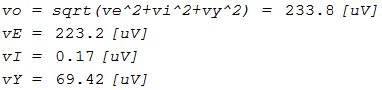
| (%i91) |
XplotdB( [10*log10(S_oe(f)/(e_R^2)), 10*log10(S_oi(f)/(e_R^2)), 10*log10(S_oy(f)/(e_R^2))], f_n1,f_n2 , ["10*log10(S_oe(f)/(e_R^2))", "10*log10(S_oi(f)/(e_R^2))", "10*log10(S_oy(f)/(e_R^2))"] ) $ |
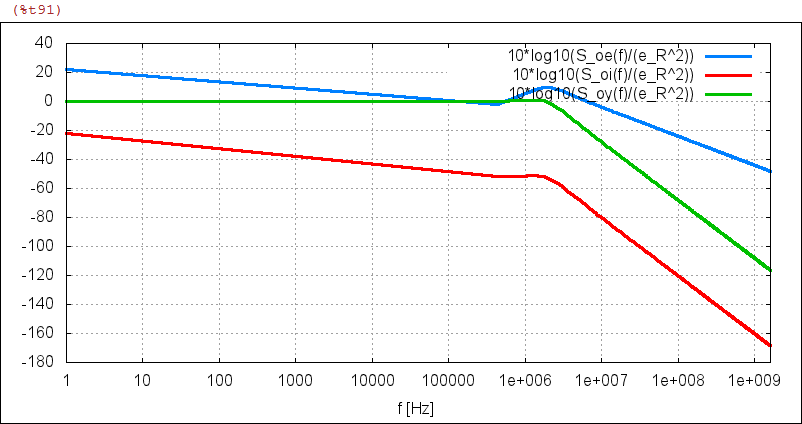
| (%i92) |
XplotdB( [20*log10(GK_n(f)), 20*log10(GM_n(f)/R2)], f_n1,f_n2 , ["20*log10(GK_n(f))", "20*log10(GM_n(f)/R2)"] ) $ |
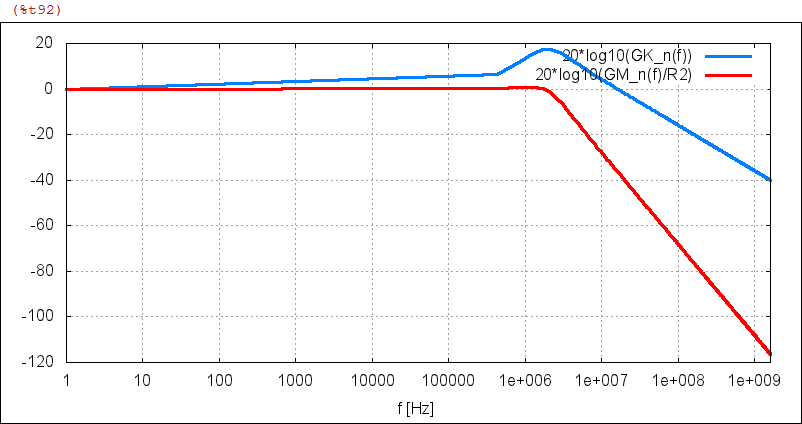
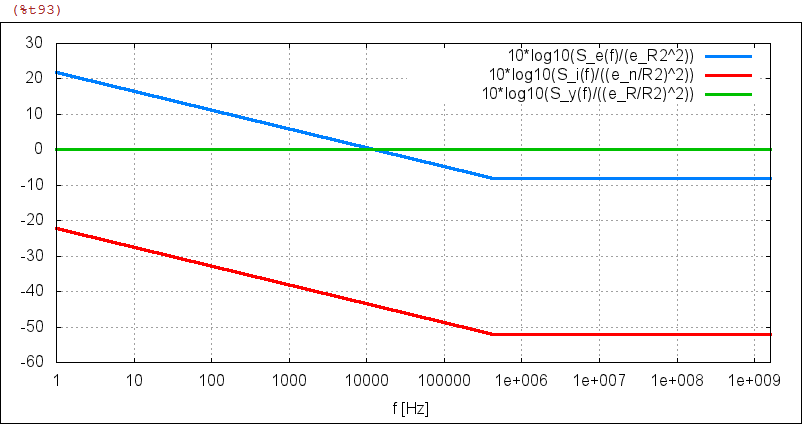
| (%i93) |
XplotdB( [10*log10(S_e(f)/(e_R^2)), 10*log10(S_i(f)/((e_R/R2)^2)), 10*log10(S_y(f)/((e_R/R2)^2))], f_n1,f_n2, ["10*log10(S_e(f)/(e_R2^2))","10*log10(S_i(f)/((e_n/R2)^2))", "10*log10(S_y(f)/((e_R/R2)^2))"] ) $ |