AS - example 3 - I/V converter stability
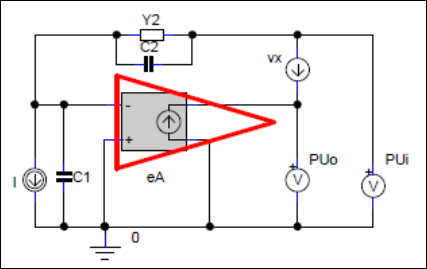
Figure 1: C:\jobs\Maxima\AS\ex\_img\ex3.png

Figure above (embedded only *.wxmx) shows model of I/V converter used in stability analysis.
| (%i1) |
/* working directory must be explicitly defined HERE ! */ kill(all) $ file_search_maxima : append(["c:/jobs/Maxima/AS/ex/libs/###.{mac,mc}"],file_search_maxima ) $ load("_myUnits") ; load("_myFunctions") ; load("_myDrawings") ; /* suppress ratsimp warnings */ ratprint: false $ algebraic:true $ keepfloat:true $ fpprintprec: 4 $ /* Debug level DBG:0 ->none, DBG:3 ->all */ DBG: 2 $ /* GNU plot (default) or wxplot for 0 */ GNUPLOTFLAG: 0 $ |

| (%i11) |
/* By default, all symbols, are considered to represent real numbers */ declare(s, complex) $ /*... AS ... */ /*... TF ... */ /* Ui=Kix*vx+Mi*I */ Da: (gi)*(s*(C2*eA+C1+C2)+Y2*eA+Y2) $ DbKix: -(gi)*(s*(C1+C2)+Y2) $ Kix:DbKix/Da $ DbMi: (gi)*(eA) $ Mi:DbMi/Da $ /*... TF ... */ /* Uo:Kox*vx+Mo*I */ DbKox: (gi)*(s*(C2*eA)+Y2*eA) $ Kox: DbKox/Da $ DbMo: (gi)*(eA) $ Mo:DbMo/Da $ /*... EndOfAS ...*/ /* OP-AMP Gain */ A(s):=(GBW/s)*(sqrt(2)/(1+s/GBW)) $ DBG_1("A(s) = ", A(s)) $ /* closed loop TF M = Uo/I */ Mo: ratsimp(Mo) $ DBG_3("Mo = ", Mo) $ Mo:subst( eA=A(s) , Mo) $ DBG_3("Mo = ", Mo) $ Mo:radcan( Mo) $ DBG_1("Mo = ", Mo) $ |
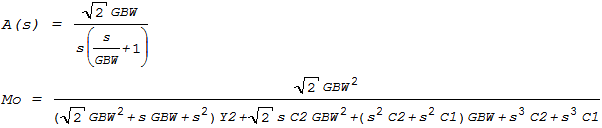
| (%i29) |
/* OPEN LOOP GAIN T = -Uo/Ui = -Kox/Kix */ Kox:subst(A,eA,Kox) $ Kix:subst(A,eA,Kix) $ T:-Kox/Kix $ b:ratsimp(T/A) $ /* OP-AMP */ ft: 16*MHz $ GBW: 2*(%pi)*ft $ /* component values */ R2: 100*kOhm $ Y2: 1/R2 $ C2: 1.4 *pF $ C1: 5.0*pF $ /* plot range */ f_plt1: 100 $ f_plt2: 100*ft $ DBG_1("ft [MHz]= ", float(ft/MHz)) $ DBG_1("R2 [kOhm]= ", R2/kOhm) $ DBG_1("C2 [pF]= ", C2/pF) $ DBG_1("C1 [pF]= ", C1/pF) $ |
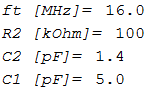
| (%i45) |
wxplot_size:[800,500] $ GA(f) := cabs(A(%i*2*%pi*f)) $ phA(f) := carg(A(%i*2*%pi*f)) $ DBGF_3(Xplot_dBx2, [20*log10(GA(f)), phA(f)/%pi], f_plt1,f_plt2,["20*log10(GA(f))", "phA(f)/%pi"] ) $ |
| (%i49) |
define( b(s), ev(b, C2=float(C2), Y2=float(Y2), C1=float(C1), GBW=float(GBW))) $ DBG_3("b(s) = ", b(s)) $ Gb(f) := cabs(b(%i*2*%pi*f)) $ phb(f) := carg(b(%i*2*%pi*f)) $ DBGF_3(Xplot_dBx2, [20*log10(Gb(f)), phb(f)/%pi], f_plt1,f_plt2,["20*log10(Gb(f))", "phb(f)/%pi"] ) $ |
| (%i54) |
/* open loop gain */ T(s):=A(s)*b(s) $ DBG_3("T(s) = ", T(s)) $ GT(f) := cabs(T(%i*2*%pi*f)) $ phT(f) := carg(T(%i*2*%pi*f)) $ DBGF_2( Xplot_dBx2, [20*log10(GT(f)), phT(f)/%pi], f_plt1,f_plt2, ["20*log10(GT(f))", "phT(f)/%pi"] ) $ |
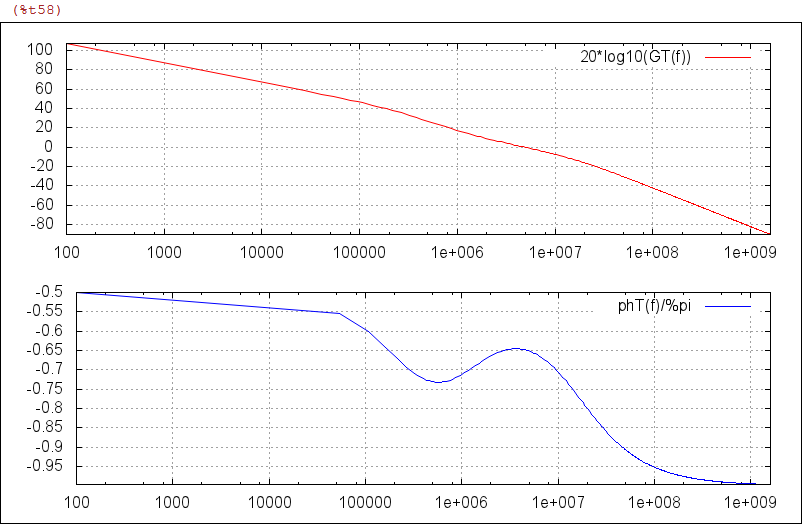
| (%i59) |
/* find phase margin */ declare(f, real) $ assume(f > 0) $ /* solve(GT(f)-1, f); */ fx:find_root(GT(f)-1, 0.1*ft, 10*ft) $ DBG_1( "fx [MHz]= ", float(fx/MHz)) $ DBG_1( "20*log10(GT(fx)) =", float(20*log10(GT(fx))) ) $ DBG_1( "phT(fx)/%pi*180 =", float(phT(fx)/%pi*180) ) $ DBG_1( "phase_margin =", float((phT(fx)+%pi)/%pi*180) ) $ |
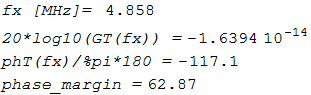
| (%i66) |
define(M(s), float(ratsimp(ev(Mo, eA=A(s), C1=float(C1), Y2=float(Y2), C2=float(C2)), s))) $ DBG_1("M(s) = ", M(s)) $ GMn(f) := float(cabs(M(%i*2*%pi*f)/R2)) $ phM(f) := float(carg(M(%i*2*%pi*f))) $ DBG_3("GMn(f) = ", GMn(f)) $ DBG_3("phM(f) = ", phM(f)) $ DBGF_2(Xplot_dBx2, [20*log10(GMn(f)), phM(f)/%pi], f_plt1,f_plt2, ["20*log10(GM(f)/R2)", "phM(f)/%pi"] ) $ |
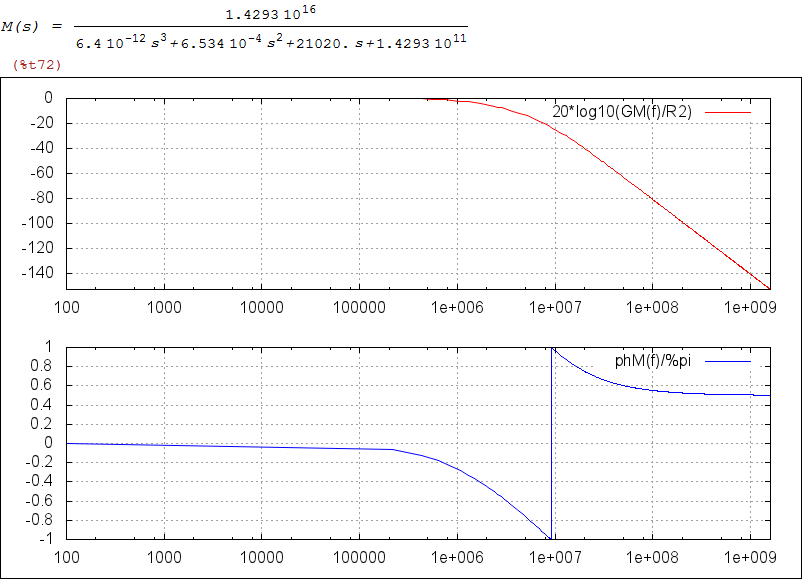
ilt - Inverse Laplace transform - expr must be a ratio of polynomials
whose denominator has only linear and quadratic factors.
This is 3rd order problem , there must be at least one real pole
| (%i73) |
MM:denom(M(s)) $ ROOTS:realroots(MM) $ b1: float(rhs(ROOTS[1])) $ DBG_3("MM= ", MM) $ /* real pole gives linear factor */ MFL: s-b1 $ DBG_3("MFL= ", MFL) $ /* quadratic factor should be get division MM = MFL*MFQ */ QR:divide(MM,MFL,s) $ MFQ:float(QR[1]) $ DBG_3("MFQ= ", float(QR[1])) $ DBG_3("MFR= ", float(QR[2])) $ /* now, denominator is factored into linear and quadratic factors. */ FMM:MFL*MFQ $ define (FMM(s), ev(FMM)) $ define(H(s), 1*uA* num(M(s))/(s*FMM(s))) $ declare(h, real) $ DBG_1("H(s) = ", H(s)) $ |

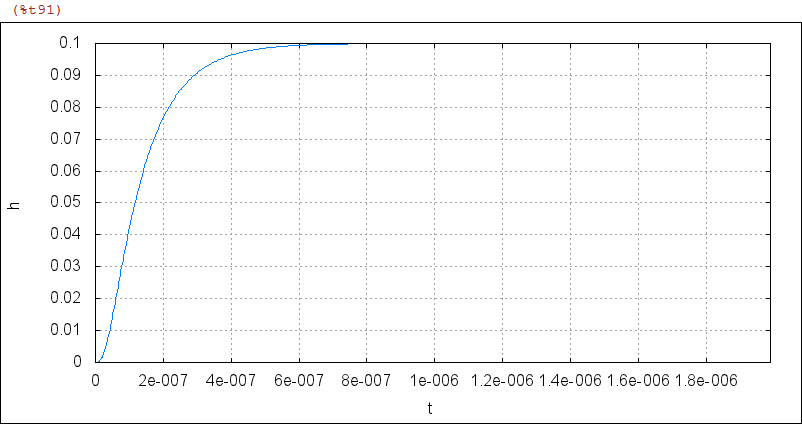
| (%i88) |
/* step response for I=1uA */ define(h(t), float(radcan(ilt(H(s),s,t)))) $ tau:float(1/(2*%pi*ft)) $ wxplot_size:[800,400] $ DBGF_1( Xplot, h,[t,0,200*tau],[gnuplot_preamble,"set grid"]) $ |