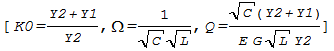
AS - example 1: tuned band-pass filter
Figure 1: C:\jobs\Maxima\AS\exp\_img\ex1.png

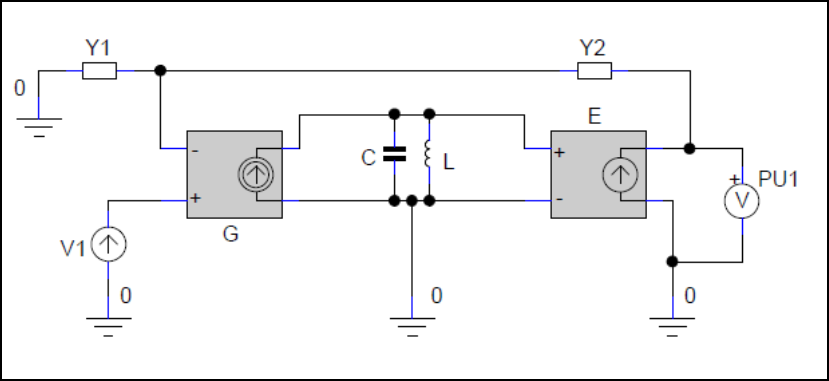
Figure above shows an ideal model of a filter (visible only in *.wxmx format)
Transfer function K = U1/V1 is simplified to get a general form.
| (%i1) |
kill(all) $ Da:(gi)*(s*(C*Y1+C*Y2)+Y2*G*E+s^(-1)*(Y2*(1/L)+Y1*(1/L))) $ Db: (gi)*(Y1*G*E+Y2*G*E) $ KU:(Db/Da) $ K:ratsimp(KU,s) $ print("K =", %) $ |
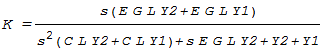
Transfer function polynomial coefficients are processed to get filter parameters.
K = KL/KM
KM = a*s^2+b*s+c
KL = d*s
KL/KM = (Ko*s*OMEGA/Q) / (s^2+s*OMEGA/Q+OMEGA^2)
| (%i6) |
KM:ratdenom(K) $ KL:ratnumer(K) $ a:ratcoef(KM,s,2) $ b:ratcoef(KM,s,1) $ c:ratcoef(KM,s,0) $ d:ratcoef(KL,s,1) $ declare([L,C,gi,G,E,Y1,Y2],real) $ assume (L > 0, C > 0, gi>0, G>0, E>0, Y1>0, Y2>0) $ eq1: K0*Omega/Q = d/a $ eq2: Omega/Q = b/a $ eq3: Omega*Omega = c/a $ soln: solve ([eq1,eq2,eq3], [K0,Omega,Q]) $ if ( rhs(soln[1][1]) > 0) then SOL: soln[1] else SOL : soln[2] $ SOL:(ratsimp(SOL)) $ print( SOL ) $ |